Archive | avril, 2020

Wiresharking MariaDB traffic

Posted on 17 avril 2020.

[SNAFU] When commenting out the ssl/tls config part in my my.cnf file [client] part I can see « mysql traffic » while logged whith a user that does not require SSL => OK

When activitating ssl/tls part config I can’t see anymore « mysql traffic » when logging in whith a user that does not require SSL/TLS => weird, no ?

image capture wireshark mariaDB

image capture wireshark mariaDB

No ! After somme times and a few searches

une pincée de sel ?

une pincée de sel ?

Posted in Inclassable0 commentaire

Protégé : RSA public key : Behind the scene

Posted on 17 avril 2020.

Cette publication est protégée par un mot de passe. Pour la voir, veuillez saisir votre mot de passe ci-dessous :

Posted in Boulot, CryptoSaisissez votre mot de passe pour accéder aux commentaires.

L’arme est d’Euler

Posted on 15 avril 2020.

A ceux qui auraient tendance à voir une référence à autre choses (20 % d’armée + 80 % d’air, par exemple) : Passez votre chemin !

En mathématiques, l’indicatrice d’Euler est une fonction de la théorie des nombres.

Elle intervient en mathématiques pures, à la fois en théorie des groupes, en théorie algébrique des nombres et en théorie analytique des nombres.

En mathématiques appliquées, à travers l’arithmétique modulaire, elle joue un rôle important en théorie de l’information et plus particulièrement en cryptologie.

La fonction indicatrice est aussi appelée fonction phi d’Euler ou simplement la fonction phi, car la lettre φ est communément utilisée pour la désigner.

Elle est nommée en l’honneur du mathématicien suisse Leonhard Euler (1707 – 1783) qui fut le premier à l’étudier.

Sommaire

  Définition et calcul explicite

  Définition et exemple

Plus formellement :

\begin{array}{ccccl}\varphi&:&\N^*&\longrightarrow&\N^*\\&&n&\longmapsto&\mathrm{card}(\{m\in\N^*~|~m\le n~\text{et}~m\text{ premier avec }n\}).\end{array}

Par exemple :

  • φ(8) = 4 car parmi les nombres de 1 à 8, seuls les quatre nombres 1, 3, 5 et 7 sont premiers avec 8,
  • φ(1) = 1 car 1 est premier avec lui-même (c’est le seul entier naturel qui vérifie cette propriété, si bien que, pour tout entier n > 1, on peut remplacer m ≤ n par m < n dans la définition ci-dessus de φ(n)).
  • φ(2) = 1.

  Premières propriétés

Articles détaillés : Groupe cyclique et Anneau Z/nZ.

Dans ce paragraphe, n désigne un entier strictement positif.

Cette propriété est démontrée dans le paragraphe Structure additive de l’article Anneau Z/nZ.

Cette propriété est démontrée dans le paragraphe Groupe des unités de l’article Anneau Z/nZ.

  • Si u et v sont deux entiers strictement positifs et premiers entre eux, alors φ(u.v)=φ(u).φ(v).

Une telle fonction est dite multiplicative. On peut démontrer cette propriété à partir du théorème des restes chinois pour les groupes, selon lequel le groupe cyclique (Z/(uv)Z,+) est isomorphe au produit (Z/uZ)×(Z/vZ). Un couple (x,y) de ce groupe produit est générateur si et seulement si x est générateur de Z/uZ et y est générateur de Z/vZ. Le nombre d’éléments générateurs du groupe produit est donc égal à φ(u).φ(v). L’isomorphisme montre que cette valeur est égale au nombre d’éléments générateurs du groupe Z/(uv)Z, ce qui démontre la formule recherchée.

  Calcul

La valeur de l’indicatrice d’Euler s’obtient par l’expression de n donnée par le théorème fondamental de l’arithmétique :

\mathrm{Si}\quad n=\prod_{i=1}^q p_i^{k_i}\quad \mathrm{alors} \quad \varphi (n)=\prod_{i=1}^q (p_i-1) p_i^{k_i-1} = n \prod_{i=1}^q {\left( 1- \frac{1}{p_i} \right) }
Dans la formule, pi désigne un nombre premier et ki un entier strictement positif.

En effet, le caractère multiplicatif de l’indicatrice d’Euler et une récurrence montrent que :

\varphi(n) = \prod_{i=1}^q \varphi(p_i^{k_i})
Il suffit alors de dénombrer le nombre d’entiers non premiers avec une puissance d’un nombre premier et plus petit que celui-ci pour remarquer que :

\forall i \in [1, q] \quad \varphi(p_i^{k_i})= p_i^{k_i} - p_i^{k_i - 1}=(p_i-1).p_i^{k_i-1}
Ce qui permet de conclure la démonstration.

  Autres propriétés

  Arithmétique modulaire

L’indicatrice d’Euler est une fonction essentielle de l’arithmétique modulaire, elle est à la base de résultats fondamentaux, à la fois en mathématiques pures et appliquées.

Cette propriété est une conséquence directe du calcul explicite de l’indicatrice.

La cryptologie utilise largement cette fonction. Le code RSA se fonde sur le théorème d’Euler, indiquant que si n est un entier strictement positif et a un entier premier avec n, alors aφ(n) ≡ 1 (mod n).

Une autre branche de la théorie de l’information utilise l’indicatrice : la théorie des codes. C’est les cas des codes correcteurs, et particulièrement des codes cycliques. Ce type de code se construit à l’aide de polynôme cyclotomique et le degré du polynôme cyclotomique Φn d’indice n à coefficients dans les entiers est égal à φ(n). Plus précisément, on dispose des égalités suivantes :

X^n-1 \ = \ \prod_{d\mid n} \Phi_d (X) \quad \mathrm{et} \ \mathrm{donc} \quad \sum_{d\mid n}\varphi(d)=n
La somme et le produit sont étendus à tous les diviseurs positifs d de n.

La formule d’inversion de Möbius permet d’inverser cette somme :

\varphi(n)=\sum_{d\mid n} d \mu(n/d)
Ici, μ désigne la fonction de Möbius usuelle définie sur l’ensemble des entiers strictement positifs, la démonstration est proposée dans l’article associé.

  Théorie analytique des nombres

Les deux fonctions génératices présentées ici sont des conséquences directes du fait que :

\sum_{d|n} \varphi(d) = n.

Une série de Dirichlet utilisant \varphi(n) est

\sum_{n=1}^{\infty} \frac{\varphi(n)}{n^s}=\frac{\zeta(s-1)}{\zeta(s)}.

qui est dérivé depuis :

\zeta(s) \sum_{n=1}^\infty \frac{\varphi(n)}{n^s} = \sum_{n=1}^\infty \left(\sum_{d|n} \varphi(d)\right) \frac{1}{n^s} = \sum_{n=1}^\infty \frac{n}{n^s} = \zeta(s-1),

ou \zeta(s) est la fonction zêta de Riemann.

Une série de Lambert utilisant \varphi(n) est

\sum_{n=1}^{\infty} \frac{\varphi(n) q^n}{1-q^n}= \frac{q}{(1-q)^2}

qui converge pour |q|<1.

dérivé de :

\sum_{n=1}^{\infty} \frac{\varphi(n) q^n}{1-q^n} = \sum_{n=1}^{\infty} \varphi(n) \sum_{r\ge 1} q^{rn}

avec

\sum_{k\ge 1} q^k \sum_{n|k} \varphi(n) = \sum_{k\ge 1} k q^k = \frac{q}{(1-q)^2}.

  Croissance de la fonction

La croissance de \varphi(n) comme une fonction de n est une question intéressante. La première impression que l’on a pour les petits n est que \varphi(n) doit être notablement plus petit que n, ce qui est quelque peu erroné. Asymptotiquement, nous avons

n^{1 - \epsilon} < \varphi(n) < n\,

pour n’importe quel \epsilon > 0\, et n > N(\epsilon)\, . En fait, si nous considérons

\frac {\varphi(n)}{n}\,

nous pouvons écrire, à partir de la formule précédente, sous forme de produit de facteurs

1 - p^{-1}\,

où les p sont des nombres premiers divisant n. Par conséquent les valeurs de n correspondantes aux valeurs particulièrement petites du rapport sont les n qui sont le produit d’un segment initial de la suite de tous les nombres premiers. À partir du théorème des nombres premiers il peut être montré qu’une constante ε dans la formule précédente peut par conséquent être remplacée par

C \frac{\log\log {n}}{{\log n}}\, .

  Les 99 premières valeurs de la fonction φ

  Les 100 premières valeurs de la fonction φ
\varphi(n) +0 +1 +2 +3 +4 +5 +6 +7 +8 +9
0+ 1 1 2 2 4 2 6 4 6
10+ 4 10 4 12 6 8 8 16 6 18
20+ 8 12 10 22 8 20 12 18 12 28
30+ 8 30 16 20 16 24 12 36 18 24
40+ 16 40 12 42 20 24 22 46 16 42
50+ 20 32 24 52 18 40 24 36 28 58
60+ 16 60 30 36 32 48 20 66 32 44
70+ 24 70 24 72 36 40 36 60 24 78
80+ 32 54 40 82 24 64 42 56 40 88
90+ 24 72 44 60 46 72 32 96 42 60

On observe que, excepté pour n = 1 ou 2, \varphi(n) est pair, propriété qui est générale. En effet, en notant n=2^k \prod_{i=1}^q p_i^{k_i} avec les p_i impairs et q éventuellement nul (produit vide), on a :

\varphi (n)=2^{k - 1} \prod_{i=1}^q (p_i-1) p_i^{k_i-1}
Or si n > 2, alors k > 1 ou q > 0. Dans un cas comme dans l’autre, on obtient bien que \varphi(n) est pair.

  Autres formules impliquant la fonction φ d’Euler

\;\varphi(n^m) = n^{m-1}\varphi(n) pour m\ge 1
\sum_{d \mid n} \frac{\mu^2(d)}{\varphi(d)} = \frac{n}{\varphi(n)}
\sum_{1\le k\le n \atop (k,n)=1}\!\!k = \frac{1}{2}n\varphi(n) pour \;n>1
\sum_{k=1}^n\varphi(k) = \frac{1}{2}\left(1+ \sum_{k=1}^n \mu(k)\left\lfloor\frac{n}{k}\right\rfloor^2\right)
\sum_{k=1}^n\frac{\varphi(k)}{k} = \sum_{k=1}^n\frac{\mu(k)}{k}\left\lfloor\frac{n}{k}\right\rfloor
\sum_{k=1}^n\frac{k}{\varphi(k)} = \mathcal{O}(n)
\sum_{k=1}^n\frac{1}{\varphi(k)} = \mathcal{O}(\log(n))

  Inégalités

Certaines inégalités impliquant la fonction \varphi(n) sont :

\varphi(n) > \frac {n} {e^\gamma\; \log \log n + \frac {3} {\log \log n}} pour n > 2, où \gamma\, est la constante d’Euler,
\varphi(n) \ge \sqrt{\frac {n} {2} } pour n > 0,

et

\varphi(n) \ge \sqrt{n} pour n > 6.

Pour un nombre premier n, clairement \varphi(n) = n-1\,. Pour un nombre composé n, nous avons

\varphi(n) \le n-\sqrt{n}

Pour tous les n>1  :

0<\frac{\varphi(n)}{n}<1

Pour un grand n aléatoire, ces bornes ne peuvent pas être encore améliorées, en effet :

\liminf \frac{\varphi(n)}{n}=0 \mbox{ et } \limsup \frac{\varphi(n)}{n}=1.

Une paire d’inégalités combinant la fonction \varphi et la fonction diviseur \sigma sont :

\frac {6 n^2}{\pi^2} < \varphi(n) \sigma(n) < n^2 \mbox{ pour } n>1.

  Conjectures

  Voir aussi

This entry is from Wikipedia, the leading user-contributed encyclopedia. It may not have been reviewed by professional editors (see full disclaimer)

© Copyright auteur(s) de Wikipédia – Cet article est sous licence CC BY-SA 3.0

Posted in Crypto0 commentaire

TLS setup for Apache Tomcat

Posted on 10 avril 2020.

Very first thing : Read That F*** Manual !

$JAVA_HOME/bin/keytool -genkey -alias tomcat -keyalg RSA

and specify a password value of « whatYouWantButNotChangeIt ».

keystore

keystore

 

 

 

 

 

 

 

 

 

 

 

 

 

Edit your server.xml file, beware that commented examples provided could be very far from what youy need :

<!-- Define an SSL Coyote HTTP/1.1 Connector on port 8443 -->
<Connector
           protocol="org.apache.coyote.http11.Http11NioProtocol"
           port="8443" maxThreads="200"
           scheme="https" secure="true" SSLEnabled="true"
           keystoreFile="${user.home}/.keystore" keystorePass="changeit"
           clientAuth="false" sslProtocol="TLS"/>


<Connector port="8443" protocol="org.apache.coyote.http11.Http11NioProtocol"
               maxThreads="150" SSLEnabled="true" scheme="https" secure="true"
keystoreFile="/root/.keystore"
keystorePass="***********"
clientAuth="false" sslProtocol="TLS">

Posted in Boulot0 commentaire

Mais pourquoi ma clé commence toujours par MIGf… ?

Posted on 06 avril 2020.

Read that f… RFC 1421 : Privacy Enhancement for Internet Electronic Mail

and follow those precious links :

https://lapo.it/asn1js
https://docs.microsoft.com/en-us/windows/win32/seccertenroll/about-encoded-length-and-value-bytes
http://javadoc.iaik.tugraz.at/iaik_jce/current/iaik/x509/PublicKeyInfo.html
https://medium.com/@bn121rajesh/understanding-rsa-public-key-70d900b1033c

# Generate 1024 bit Private key
$ openssl genrsa -out myprivate.pem 1024
# Separate the public part from the Private key file.
$ openssl rsa -in myprivate.pem -pubout > mypublic.pem
# Display the contents of private key
$ cat myprivate.pem

-----BEGIN RSA PRIVATE KEY-----
MIICXQIBAAKBgQDRFNU++93aEvz3cV8LSUP9ib3iUxT7SufdVXcgVFK9M3BYzvro
A1uO/parFOJABTkNhTPPP/6mjrU2CPEZJ1zIkpaSNJrrhpp/rNMO9nyLYPGs9Mfd
BiWUPmHW5mY1oD0ye4my0tEsHOlgHC8AhA8OtiHr6IY0agXmH/y5YmSWbwIDAQAB
AoGAAj/IH3pUI6FqqTrF+/gYzCRsL4AXTLC8l8vwkR93GGPyRHJNjqtik8I3WrXJ
zUiBGZ0iNouIsL/+QQuNlGiw/c5i2X3nTntREDS9xs2M0x+MWD/5qI1sn0Qk0HNP
BbDczlvO8wXNFGIHiTiPVEawoeNwhMqJDyGcbsEOZp2pLokCQQDvlMBU6dOeOP9a
jnENFSlrvzNR0nugFeoGmfq6s4Czz2QtUd9baKqBfEBSdJskwFVHgxbFA1Dc7iFu
rJkoQEeFAkEA32j9ibSVryxLvWUZngKNwo2xE+wcYDAYVBMsYC3OBU3FXhVkFD06
ZVnJsY/4bd2VdQI+bI2KV99aHutMJG2WYwJABMn2ZjweTMVa5VZ/kAFiSJMT1Yjd
i7+kY+lkB6Na6T02BWnjixI2hkwThRJrn3pwufM2201Lqn7gEDRHA3T1eQJBAKZG
1RUNo6558HEo8vUIf4vCu33RaJkqkqDYmFmJHeISrQfGMfNiUrkmJ5iRR9w1ZExu
/Bj9C281XDTQ+Z3PNnMCQQCan+pvj0OZH6o0PAMJGBBwRECPpfZ6mUjwA2YD3g61
MHjtIYmKKGmn64Qs8zQ4mNEDboQqyaov3Ij/I6c0ZQlc
-----END RSA PRIVATE KEY-----

Privacy Enhanced Mail (PEM)

Privacy Enhanced Mail (PEM) is a Base64 encoded Distinguished Encoding Rules(DER)
PEM file is human readable as it uses 64 printable characters for encoding.
It is easy to share PEM file.

 

Display the contents of public key PEM file

# Display the contents of public key PEM file
$ cat mypublic.pem

-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDRFNU++93aEvz3cV8LSUP9ib3i
UxT7SufdVXcgVFK9M3BYzvroA1uO/parFOJABTkNhTPPP/6mjrU2CPEZJ1zIkpaS
NJrrhpp/rNMO9nyLYPGs9MfdBiWUPmHW5mY1oD0ye4my0tEsHOlgHC8AhA8OtiHr
6IY0agXmH/y5YmSWbwIDAQAB
-----END PUBLIC KEY-----

 

Distinguished Encoding Rules (DER) format of public key

DER is encoded in Type-Length-Value (TLV) format.
DER is in binary format for PEM file and follows certain structure for public key.

# Convert PEM file to DER format using openssl rsa
$ openssl rsa -pubin -inform PEM -in mypublic.pem -outform DER -out mypublic.der
# Dump the DER file in hex format.
$ xxd -g 1 -u mypublic.der | cut -c -57
00000000: 30 81 9F 30 0D 06 09 2A 86 48 86 F7 0D 01 01 01
00000010: 05 00 03 81 8D 00 30 81 89 02 81 81 00 D1 14 D5
00000020: 3E FB DD DA 12 FC F7 71 5F 0B 49 43 FD 89 BD E2
00000030: 53 14 FB 4A E7 DD 55 77 20 54 52 BD 33 70 58 CE
00000040: FA E8 03 5B 8E FE 96 AB 14 E2 40 05 39 0D 85 33
00000050: CF 3F FE A6 8E B5 36 08 F1 19 27 5C C8 92 96 92
00000060: 34 9A EB 86 9A 7F AC D3 0E F6 7C 8B 60 F1 AC F4
00000070: C7 DD 06 25 94 3E 61 D6 E6 66 35 A0 3D 32 7B 89
00000080: B2 D2 D1 2C 1C E9 60 1C 2F 00 84 0F 0E B6 21 EB
00000090: E8 86 34 6A 05 E6 1F FC B9 62 64 96 6F 02 03 01
000000a0: 00 01

 

Structured DER file content

1:30 81 9F // Type: 30 (SEQUENCE) Length: 0x9F
2:| 30 0D // Type: 30 (SEQUENCE) Length: 0x0D
3:| | 06 09 // Type: 06 (OBJECT_IDENTIFIER) Length: 0x09
4:| | - 2A 86 48 // 9 bytes OID value. HEX encoding of
5:| | - 86 F7 0D // 1.2.840.113549.1.1.1
6:| | - 01 01 01
7:| | 05 00 // Type: 05 (NULL) Length: 0x00
8:| 03 81 8D // Type: 03 (BIT STRING) Length: 0x8D
9:| | - 00 // Number of unused bits in last content byte
10:| | 30 81 89 // Type: 30 (SEQUENCE) Length: 0x89
11:| | | 02 81 81 // Type: 02 (INTEGER) Length: 0x81
12:| | | - 00 // Leading ZERO of integer
13:| | | - D1 14 D5 3E FB DD DA 12 FC F7 71 5F 0B 49 43 FD
14:| | | - 89 BD E2 53 14 FB 4A E7 DD 55 77 20 54 52 BD 33
15:| | | - 70 58 CE FA E8 03 5B 8E FE 96 AB 14 E2 40 05 39
16:| | | - 0D 85 33 CF 3F FE A6 8E B5 36 08 F1 19 27 5C C8
17:| | | - 92 96 92 34 9A EB 86 9A 7F AC D3 0E F6 7C 8B 60
18:| | | - F1 AC F4 C7 DD 06 25 94 3E 61 D6 E6 66 35 A0 3D
19:| | | - 32 7B 89 B2 D2 D1 2C 1C E9 60 1C 2F 00 84 0F 0E
20:| | | - B6 21 EB E8 86 34 6A 05 E6 1F FC B9 62 64 96 6F
21:| | | 02 03 // Type: 02 (INTEGER) Length: 0x3
22:| | | - 01 00 01 // Public Exponent. Hex for 65537

 

DER file contains Object Identifier, Modulus and Public exponent in HEX format.

Lines 4, 5, 6 is the HEX encoding of OID.
Lines 13 to 20 is the modulus (n).
Line 22 is the public exponent.

You can also have a look at Lapo ASN.1 javascript decoder :

Javascript ASN.1 decoder

Javascript ASN.1 decoder

Modulus and Public exponent from public key using openssl

# Get Modulus and Public exponent from public PEM file
$ openssl rsa -pubin -inform PEM -text -noout < mypublic.pem

Public-Key: (1024 bit)
Modulus:
00:d1:14:d5:3e:fb:dd:da:12:fc:f7:71:5f:0b:49:
43:fd:89:bd:e2:53:14:fb:4a:e7:dd:55:77:20:54:
52:bd:33:70:58:ce:fa:e8:03:5b:8e:fe:96:ab:14:
e2:40:05:39:0d:85:33:cf:3f:fe:a6:8e:b5:36:08:
f1:19:27:5c:c8:92:96:92:34:9a:eb:86:9a:7f:ac:
d3:0e:f6:7c:8b:60:f1:ac:f4:c7:dd:06:25:94:3e:
61:d6:e6:66:35:a0:3d:32:7b:89:b2:d2:d1:2c:1c:
e9:60:1c:2f:00:84:0f:0e:b6:21:eb:e8:86:34:6a:
05:e6:1f:fc:b9:62:64:96:6f
Exponent: 65537 (0x10001)

Exponent and modulus printed by openssl rsa matches with the Public exponent and modulus from DER file content.

More information on recommended syntax for interchanging RSA public keys between implementations is given in Appendix A.1.1 of rfc3447 ( PKCS#1);

RSA key representation

RSA key representation

 

Object Identifier

OID describes the object. It is a series of nodes separated by period.

OID Value: 1.2.840.113549.1.1.1

OID description: Identifier for RSA encryption for use with Public Key Cryptosystem One defined by RSA Inc.

OID Encoding rules:

1 – The first two nodes of the OID are encoded onto a single byte. The first node is multiplied by the decimal 40 and the result is added to the value of the second node.
2 – Node values less than or equal to 127 are encoded on one byte.
3 – Node values greater than or equal to 128 are encoded on multiple bytes. Bit 7 of all bytes except the rightmost byte is set to one. Bits 0 through 6 of each byte contains the encoded value.

OID Encoding Example © Rajesh Bondugula

OID Encoding Example © Rajesh Bondugula

 

Representing length in ASN.1 encoding

If number of value bytes is < 128 (0x80) then length is represented in 1 byte. In this case most significant bit is 0. (Ex: Line 2: 0x81=10000001 => 1 octet, Line 3 in structured DER content above)

If number of value bytes is >= 128 (0x80) then length is represented in multiple bytes. Most significant bit (bit 7) of first byte is 1 indicating multiple byte length. Bits 0–6 represent number of subsequent bytes for length. (Ex:  Line 1: 0x82=10000010 => 2 octets, Line 4 in structured DER content above)

 

References

DER encoding of ASN.1 types (MSDN)
Public Key Info structure (Java doc)

 

[ajout de août 2021 suite plaintes]

– Mais du coup … tu n’as pas répondu  la question ?
[lm] C’est pas faux, mais si tu révises le fonctionnement de l’encodage base 64, à partir d’un contenu DER qui commence toujours par la même syntaxe:

xxd -r -p <<<30819F | base64
MIGf

 

Posted in Crypto, PKI, ICP, IGC1 Commentaire

Protégé : solutions

Posted on 03 avril 2020.

Cette publication est protégée par un mot de passe. Pour la voir, veuillez saisir votre mot de passe ci-dessous :

Posted in InclassableSaisissez votre mot de passe pour accéder aux commentaires.

RSA Cryptosystem overview

Posted on 01 avril 2020.

Juste besoin de cet execellent passage de Wikipedia (20200401)

RSA (Rivest–Shamir–Adleman) is one of the first public-key cryptosystems and is widely used for secure data transmission. In such a cryptosystem, the encryption key is public and distinct from the decryption key which is kept secret (private). In RSA, this asymmetry is based on the practical difficulty of factoring the product of two large prime numbers, the « factoring problem« . The acronym RSA is the initial letters of the surnames of Ron Rivest, Adi Shamir, and Leonard Adleman, who publicly described the algorithm in 1977. Clifford Cocks, an English mathematician working for the British intelligence agency Government Communications Headquarters (GCHQ), had developed an equivalent system in 1973, which was not declassified until 1997.[1]

A user of RSA creates and then publishes a public key based on two large prime numbers, along with an auxiliary value. The prime numbers must be kept secret. Anyone can use the public key to encrypt a message, but only someone with knowledge of the prime numbers can decode the message.[2] Breaking RSA encryption is known as the RSA problem. Whether it is as difficult as the factoring problem is an open question. There are no published methods to defeat the system if a large enough key is used.

RSA is a relatively slow algorithm, and because of this, it is less commonly used to directly encrypt user data. More often, RSA passes encrypted shared keys for symmetric key cryptography which in turn can perform bulk encryption-decryption operations at much higher speed.

 

Posted in Inclassable0 commentaire

Protégé : RSA avec openSSL (petits exercices)

Posted on 01 avril 2020.

Cette publication est protégée par un mot de passe. Pour la voir, veuillez saisir votre mot de passe ci-dessous :

Posted in InclassableSaisissez votre mot de passe pour accéder aux commentaires.

RSA avec openSSL

Posted on 01 avril 2020.

Intégralement et honteusement pompé sur https://www.fil.univ-lille1.fr/~wegrzyno/portail/PAC/Doc/TP-Certificats/tp-certif002.html

1. Génération d’une paire de clés

On peut générer une paire de clés RSA avec la commande genrsa de openSSL.

$ openssl genrsa -out <fichier> <taille>

où fichier est un nom de fichier de sauvegarde de la clé, et taille et la taille souhaitée (exprimée en bits) du modulus de la clé.

Par exemple, pour générer une paire de clés de 1024 bits, stockée dans le fichier maCle.pem, on tape la commande

$ openssl genrsa -out maCle.pem 1024

Le fichier obtenu est un fichier au format PEM (Privacy Enhanced Mail, format en base 64), dont voici un exemple :

$ cat maCle.pem

-----BEGIN RSA PRIVATE KEY----- MIICXAIBAAKBgQCveVjLltevTC5kSAiTYjHMVuAR80DHMLWCp3BOVZ49eXwraXxO 7AfKWpA5g0wFZgZNERIfFYaCnvaQDQA+9BRIfsSSr3oSw0My5SD6eg15v0VmJmvP d8LgBypJHbr6f5MXWqntvzp0Qvg6ddeNpUIrqkkh4uDfHFDWqyrkQUCvKwIDAQAB AoGANchUrfnq28DWy0fE0R+cscvC292Z8jN8vrIBWxEk8iSlKU0om6v+a0g8wlP6 3gC6V66uxjY7xxdf7SD+/UykVl4PGFymhLtywSdGlgec3tLgBtV3ytJFilAVDBij LzQwUegCO4zt1JWYc6vvaVdNyQSaGIIeYGsNDWEYlOtDSlkCQQDVRn9JS15G8p+H
4Z0PbU9ZQg2L1u9/SD/kELVe3Kx1fdHulxH0v8V2AgPdXA29Nhi+TxUtC+V8CMc2 KXmAvFsHAkEA0qBDmjHMDPwcGaqbQ2lymYQIGlZ5TLQFA98Dey2uE+CB6pmS/e/Z ilu1IaasuE3vBzXfB/JU7DUkV++JQ7TtvQJBAL2s5dUch2sXqlOhjhpDP/eE7CE6 9WLAsbm2Nmd4YJRZYtQLXPfLeeSapC9BCCMHsnfGQ3H9i4mFEQ6VUi7w1Q8CQAQa pVaS09QI8Y86eM4GdvowzWud9b0d4N8jcFDtIfA3NrDYjzmte8KraMsgEUuCET9F
uHPSL/9uRagE/dq44s0CQCMQU4PMqkMtwzCFsV8ZqLmkDPn1binIAwRLYFcsQRDt gTi6rycz3Pk1hCVzBfyMd8zwqpwKmR5FoOXuJEv+mVg=
-----END RSA PRIVATE KEY-----

2. Visualisation des clés RSA

La commande rsa permet de visualiser le contenu d’un fichier au format PEM contenant une paire de clés RSA.

$ openssl rsa -in <fichier> -text -noout

L’option -text demande l’affichage décodé de la paire de clés. L’option -noout supprime la sortie normalement produite par la commande rsa.

Par exemple

$ openssl rsa -in maCle.pem -text -noout

Private-Key: (1024 bit)
modulus:
00:af:79:58:cb:96:d7:af:4c:2e:64:48:08:93:62: 31:cc:56:e0:11:f3:40:c7:30:b5:82:a7:70:4e:55: 9e:3d:79:7c:2b:69:7c:4e:ec:07:ca:5a:90:39:83: 4c:05:66:06:4d:11:12:1f:15:86:82:9e:f6:90:0d: 00:3e:f4:14:48:7e:c4:92:af:7a:12:c3:43:32:e5: 20:fa:7a:0d:79:bf:45:66:26:6b:cf:77:c2:e0:07: 2a:49:1d:ba:fa:7f:93:17:5a:a9:ed:bf:3a:74:42: f8:3a:75:d7:8d:a5:42:2b:aa:49:21:e2:e0:df:1c:
50:d6:ab:2a:e4:41:40:af:2b
publicExponent: 65537 (0x10001)
privateExponent:
35:c8:54:ad:f9:ea:db:c0:d6:cb:47:c4:d1:1f:9c: b1:cb:c2:db:dd:99:f2:33:7c:be:b2:01:5b:11:24: f2:24:a5:29:4d:28:9b:ab:fe:6b:48:3c:c2:53:fa: de:00:ba:57:ae:ae:c6:36:3b:c7:17:5f:ed:20:fe: fd:4c:a4:56:5e:0f:18:5c:a6:84:bb:72:c1:27:46: 96:07:9c:de:d2:e0:06:d5:77:ca:d2:45:8a:50:15: 0c:18:a3:2f:34:30:51:e8:02:3b:8c:ed:d4:95:98: 73:ab:ef:69:57:4d:c9:04:9a:18:82:1e:60:6b:0d:
0d:61:18:94:eb:43:4a:59
prime1:
00:d5:46:7f:49:4b:5e:46:f2:9f:87:e1:9d:0f:6d: 4f:59:42:0d:8b:d6:ef:7f:48:3f:e4:10:b5:5e:dc: ac:75:7d:d1:ee:97:11:f4:bf:c5:76:02:03:dd:5c: 0d:bd:36:18:be:4f:15:2d:0b:e5:7c:08:c7:36:29:
79:80:bc:5b:07
prime2:
00:d2:a0:43:9a:31:cc:0c:fc:1c:19:aa:9b:43:69: 72:99:84:08:1a:56:79:4c:b4:05:03:df:03:7b:2d: ae:13:e0:81:ea:99:92:fd:ef:d9:8a:5b:b5:21:a6: ac:b8:4d:ef:07:35:df:07:f2:54:ec:35:24:57:ef:
89:43:b4:ed:bd
exponent1:
00:bd:ac:e5:d5:1c:87:6b:17:aa:53:a1:8e:1a:43: 3f:f7:84:ec:21:3a:f5:62:c0:b1:b9:b6:36:67:78: 60:94:59:62:d4:0b:5c:f7:cb:79:e4:9a:a4:2f:41: 08:23:07:b2:77:c6:43:71:fd:8b:89:85:11:0e:95:
52:2e:f0:d5:0f
exponent2:
04:1a:a5:56:92:d3:d4:08:f1:8f:3a:78:ce:06:76: fa:30:cd:6b:9d:f5:bd:1d:e0:df:23:70:50:ed:21: f0:37:36:b0:d8:8f:39:ad:7b:c2:ab:68:cb:20:11: 4b:82:11:3f:45:b8:73:d2:2f:ff:6e:45:a8:04:fd:
da:b8:e2:cd
coefficient:
23:10:53:83:cc:aa:43:2d:c3:30:85:b1:5f:19:a8: b9:a4:0c:f9:f5:6e:29:c8:03:04:4b:60:57:2c:41: 10:ed:81:38:ba:af:27:33:dc:f9:35:84:25:73:05: fc:8c:77:cc:f0:aa:9c:0a:99:1e:45:a0:e5:ee:24:
4b:fe:99:58

Les différents éléments de la clé sont affichés en hexadécimal (hormis l’exposant public). On peut distinguer le modulus, l’exposant public (qui par défaut est toujours 655371), l’exposant privé, les nombres premiers facteurs du modulus, plus trois autres nombres qui servent à optimiser l’algorithme de déchiffrement.

On vérifie assez facilement avec 2 lignes de java que les 2 nombres premiers p et q font bien 1024 bits et que le modulus n = p x q

Playing with big numbers

Playing with big numbers

3. Chiffrement d’un fichier de clés RSA

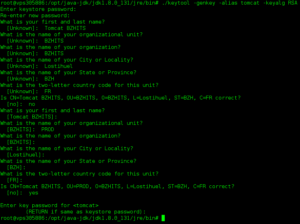
Il n’est pas prudent de laisser une paire de clés en clair (surtout la partie privée). Avec la commande rsa, il est possible de chiffrer une paire de clés2. Pour cela trois options sont possibles qui précisent l’algorithme de chiffrement symétrique à utiliser : -des, -des3 et -idea.

$ openssl rsa -in maCle.pem -des3 -out maCle.pem writing RSA key Enter PEM pass phrase: Verifying - Enter PEM pass phrase:

Une phrase de passe est demandée deux fois pour générer une clé symétrique protégeant l’accès à la clé.

4. Export de la partie publique

La partie publique d’une paire de clés RSA est publique, et à ce titre peut être communiquée à n’importe qui. Le fichier maCle.pem contient la partie privée de la clé, et ne peut donc pas être communiqué tel quel (même s’il est chiffré). Avec l’option -pubout on peut exporter la partie publique d’une clé.

$ openssl rsa -in maCle.pem -pubout -out maClePublique.pem

-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQCveVjLltevTC5kSAiTYjHMVuAR
80DHMLWCp3BOVZ49eXwraXxO7AfKWpA5g0wFZgZNERIfFYaCnvaQDQA+9BRIfsSS
r3oSw0My5SD6eg15v0VmJmvPd8LgBypJHbr6f5MXWqntvzp0Qvg6ddeNpUIrqkkh
4uDfHFDWqyrkQUCvKwIDAQAB
-----END PUBLIC KEY-----

Mais pourquoi ma clé commence toujours par MIGf… ?


# openssl rsa -inform PEM -pubin -in maClePublique.pem -text -noout
Public-Key: (1024 bit)
Modulus:
00:af:79:58:cb:96:d7:af:4c:2e:64:48:08:93:62:
31:cc:56:e0:11:f3:40:c7:30:b5:82:a7:70:4e:55:
9e:3d:79:7c:2b:69:7c:4e:ec:07:ca:5a:90:39:83:
4c:05:66:06:4d:11:12:1f:15:86:82:9e:f6:90:0d:
00:3e:f4:14:48:7e:c4:92:af:7a:12:c3:43:32:e5:
20:fa:7a:0d:79:bf:45:66:26:6b:cf:77:c2:e0:07:
2a:49:1d:ba:fa:7f:93:17:5a:a9:ed:bf:3a:74:42:
f8:3a:75:d7:8d:a5:42:2b:aa:49:21:e2:e0:df:1c:
50:d6:ab:2a:e4:41:40:af:2b
Exponent: 65537 (0x10001)

 

5. Chiffrement / déchiffrement de données avec RSA

On peut chiffrer des données avec une clé RSA. Pour cela on utilise la commande rsautl

$ openssl rsautl -encrypt -in <fichier_entree> -inkey <cle> \ -out <fichier_sortie

où

  • fichier_entree est le fichier des données à chiffrer. Attention, le fichier des données à chiffrer ne doit pas avoir une taille excessive (ne doit pas dépasser 116 octets pour une clé de 1024 bits).
  • cle est le fichier contenant la clé RSA. Si ce fichier ne contient que la parte publique de la clé, il faut rajouter l’option -pubin.
  • fichier_sortie est le fichier de données chiffré.

Pour déchiffrer on remplace l’option -encrypt par -decrypt. Le fichier contenant la clé doit évidemment contenir la partie privée.

6. Signature de fichiers

La commande dgst permet de le faire.

$ openssl dgst <hachage> -out <empreinte> <fichier_entree>

où hachage est une fonction de hachage. Avec openssl, plusieurs fonctions de hachage sont proposées dont

  • MD5 (option -md5), qui calcule des empreintes de 128 bits,
  • SHA1 (option -sha1), qui calcule des empreintes de 160 bits,
  • RIPEMD160 (option -ripemd160), qui calcule des empreintes de 160 bits.

Dans la vraie vie signer un document revient à chiffrer son empreinte (et non pas à signer son empreinte comme on peut le lire dans le doc original, puisque la signature est une double opération cryptographique hash&encrypt). Pour cela, on utilise l’option -sign de la commande rsautl

$ openssl rsautl -sign -in <empreinte> \ -inkey <cle> \ -out <signature>

et pour vérifier la signature

$ openssl rsautl -verify -in <signature> -pubin \ -inkey <cle> -out <empreinte

Il reste ensuite à vérifier que l’empreinte ainsi produite est la même que celle que l’on peut calculer. L’option -pubin indique que la clé utilisée pour la vérification est la partie publique de la clé utilisée pour la signature.

Pour ceux qui ne veulent pas jouer avec  Java : Command Line Utilities openSSL

Si vous voulez faire des tests en ligne (! confidentialité sur clefs privées), il existe de nombreux outils :
– https://8gwifi.org/ – PEM Parseur
– https://www.devglan.com/online-tools/rsa-encryption-decryption
– https://www.sslshopper.com/ssl-certificate-tools.html

Si vous voulez jeter un oeil sur une conf un peu trop provoc’ à mon goût : « Fuck RSA @SummerCon2019 »

Posted in Boulot0 commentaire

RSA encryption and decryption in Java

Posted on 01 avril 2020.

A few basics about RSA (Rivest – Shamir – Adleman) cryptography encryption and decryption in java. Just for comparison with what we habitually do with openSSL without understanding any command 🙂

Check it online.

Reminder : RSA is an Asymmetric encryption technique that uses two different keys as public and private keys to perform the encryption and decryption. With RSA, you can encrypt sensitive information with a public key and a matching private key is used to decrypt the encrypted message. See details on RSA Cryptosystem on Wikipedia.

Public and private keys generation using KeyPairGenerator and asymmetric encryption and decryption with these keys.

https://github.com/bcgit

https://github.com/anishnath/crypto-tool

https://github.com/jaysridhar/java-stuff

How to Generate RSA Keys in Java

Posted in Inclassable0 commentaire


Agenda

avril 2020
L M M J V S D
 12345
6789101112
13141516171819
20212223242526
27282930